Kuartil untuk Data Tunggal-Soal dan Pembahasannya

Kuartil untuk Data Tunggal

Untuk suatu data yang telah diurutkan dengan ukuran data n ≥ 4 dapat ditentukan tiga buah nilai yang membagi data itu menjadi empat bagian yang sama banyaknya. Tiga buah nilai itu dinamakan kuartil, yaitu kuartil pertama atau kuartil bawah (Q₁), kuartil kedua atau kuartil tengah atau median (Q₂ atau Me), dan kuartil ketiga atau kuartil atas (Q₃).

Misalkan suatu data dengan ukuran n yang terdiri atas kumpulan nilai datum yang telah diurutkan berdasarkan besarnya x₁, x₂, x_3, . . ., x_n , dengan x₁ < x₂ < x₃ <_, . . ., x_n , maka kuartil bawah Q₁, kuartil tengah Q₂ , dan kuartil atas Q₃ dapat ditentukan dengan dua strategi berikut:

• Strategi dengan Menggunakan Bagan

Letak kuartil bawah Q₁, kuarti tengah Q₂ , dan kuartil atas Q₃ , dapat diperlihatlkan menggunakan bagan di bawah ini.

Selanjutnya kita menentukan kuartil-kuartil dari data itu, sebaai berikut:

1. Setelah nilai data diurutkan, kemudian ditentukan kuartil tengah Q₂ atau Median (Me)
2. Setelah didapat kuartil tengah Q₂ atau Me, kemudian kuartil bawah Q1 ditentukan oleh median dari n/2 data yang nilainya ≥ Q₂ .

• Strategi dengan Menggunakan Rumus

Bukti:

Kuartil Bawah: 

$Q_{1}=\left\{\begin{matrix}x_{\frac{1}{4}(n+1)}, untuk \ n \ ganjil\\ x_{\frac{1}{4}(n+2)}, untuk \ n \ genap\end{matrix}\right.$

Kuartil Tengah (median): Q₂ atau Me

$Q_{2}= M_{e}=\left\{\begin{matrix}x_{\frac{1}{2}(n+1)}, untuk \ n \ ganjil\\ \frac{1}{2}\left (x_{\frac{n}{2}} + x_{(\frac{n}{2}+1)} \right ), untuk \ n \ genap\end{matrix}\right.$

Kuartil Atas: 

$Q_{3}=\left\{\begin{matrix}x_{\frac{3}{4}(n+1)}, untuk \ n \ ganjil\\ x_{\frac{1}{4}(3n+2)}, untuk \ n \ genap\end{matrix}\right.$

Contoh Soal 1

Tentukan kuartil bawah, kuartil tengah (median), dan kuartil atas dari setiap data berikut ini.

a. 15, 6, 21, 4, 12, 24, 9

b. 14, 7, 5, 12, 19, 16

c. 7, 6, 2, 5, 11, 9, 12, 6

d. 5, 6, 11, 6, 9, 9, 10, 10, 12, 6, 5, 7, 14, 10

Solusi:

a. Strategi 1: menggunakan bagan

Nilai yang diurutkan:

Kuartil bawah: Q₁ = 6

Kuartil tengah: Q₂ = 12

Kuartil atas: Q₃ = 21

Strategi 2: Menggunakan rumus:

ukuran data n = 7 (ganjil)

Kuartil Bawah: 

$Q_{1}=x_{\frac{1}{4}(n+1)} = x_{\frac{1}{4}(7+1)} = x_{2} = 6$

Kuartil Tengah (median): Q₂ atau Me

$Q_{2}=x_{\frac{1}{2}(n+1)} = x_{\frac{1}{2}(7+1)} = x_{4} = 12$

Kuartil Atas: 

$Q_{3}=x_{\frac{3}{4}(n+1)} = x_{\frac{3}{4}(7+1)} = x_{6} = 21$

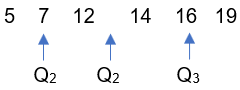
b. Strategi 1: menggunakan bagan

Nilai yang diurutkan:

Kuartil bawah: Q₁ = 7

Kuartil tengah: Q₂ = 1/2(12 + 14) = 13

Kuartil atas: Q₃ = 16

Strategi 2: Menggunakan rumus:

ukuran data n = 6 (genap)

Kuartil Bawah: 

$Q_{1}=x_{\frac{1}{4}(n+2)} = x_{\frac{1}{4}(6+2)} = x_{2} = 7$

Kuartil Tengah (median): Q₂ atau Me

$Q_{2}=\frac{1}{2}\left (x_{\frac{n}{2}} + x_{(\frac{n}{2}+1)} \right )$

$Q_{2}=\frac{1}{2}\left (x_{\frac{6}{2}} + x_{(\frac{6}{2}+1)} \right )$

$Q_{2}=\frac{1}{2}\left (x_{3} + x_{4} \right )$

$Q_{2}=\frac{1}{2}\left (12 + 14 \right )=13$

Kuartil Atas: 

$Q_{3}=x_{\frac{1}{4}(3n+2)} = x_{\frac{1}{4}(18+2)} = x_{5} = 16$

c. Strategi 1: menggunakan bagan

Nilai yang diurutkan:

Kuartil bawah: $Q_{1}=\frac{1}{2}(5+6)=5\frac{1}{2}$

Kuartil tengah: $Q_{2}=\frac{1}{2}(5+7)=6\frac{1}{2}$

Kuartil atas: $Q_{3}=\frac{1}{2}(9+11)=10$

Strategi 2: Menggunakan rumus:

ukuran data n = 8 (genap)

Kuartil Bawah: 

$Q_{1}=x_{\frac{1}{4}(n+2)} = x_{\frac{1}{4}(8+2)} = x_{2\frac{1}{2}}$

$Q_{1}=x_{2} + \frac{1}{2}(x_{3}-x_{2})$

$Q_{1}=5 + \frac{1}{2}(6-5) = 5\frac{1}{2}$

Kuartil Tengah (median): Q₂ atau Me

$Q_{2}=\frac{1}{2}\left (x_{\frac{n}{2}} + x_{(\frac{n}{2}+1)} \right )$

$Q_{2}=\frac{1}{2}\left (x_{\frac{8}{2}} + x_{(\frac{8}{2}+1)} \right )$

$Q_{2}=\frac{1}{2}\left (x_{4} + x_{5} \right )$

$Q_{2}=\frac{1}{2}\left (6 + 7 \right )=6\frac{1}{2}$

Kuartil Atas: 

$Q_{3}=x_{\frac{1}{4}(3n+2)} = x_{\frac{1}{4}(24+2)} = x_{6\frac{1}{2}}$

$Q_{3}=x_{6} + \frac{1}{2}(x_{7}-x_{6})$

$Q_{3}=9 + \frac{1}{2}(11-9) = 10$

Location:

Share :